原题链接:
洛谷P4568
题目描述
Alice 和 Bob 现在要乘飞机旅行,他们选择了一家相对便宜的航空公司。该航空公司一共在 $n$ 个城市设有业务,设这些城市分别标记为 $0$ 到 $n-1$,一共有 $m$ 种航线,每种航线连接两个城市,并且航线有一定的价格。
Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市,途中可以进行转机。航空公司对他们这次旅行也推出优惠,他们可以免费在最多 $k$ 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少?
输入格式
第一行三个整数 $n,m,k$,分别表示城市数,航线数和免费乘坐次数。
接下来一行两个整数 $s,t$,分别表示他们出行的起点城市编号和终点城市编号。
接下来 $m$ 行,每行三个整数 $a,b,c$,表示存在一种航线,能从城市 $a$ 到达城市 $b$,或从城市 $b$ 到达城市 $a$,价格为 $c$。
输出格式
输出一行一个整数,为最少花费。
样例 #1
样例输入 #1
5 6 1
0 4
0 1 5
1 2 5
2 3 5
3 4 5
2 3 3
0 2 100
样例输出 #1
8
提示
数据规模与约定
对于 $30\%$ 的数据,$2 \le n \le 50$,$1 \le m \le 300$,$k=0$。
对于 $50\%$ 的数据,$2 \le n \le 600$,$1 \le m \le 6\times10^3$,$0 \le k \le 1$。
对于 $100\%$ 的数据,$2 \le n \le 10^4$,$1 \le m \le 5\times 10^4$,$0 \le k \le 10$,$0\le s,t,a,b < n$,$a\ne b$,$0\le c\le 10^3$。
另外存在一组 hack 数据。
解法
思路1:贪心
按照原图求出最短路径的花费,然后将最短路上的各个花费由大到小排序,减去前k大的花费。
很容易就能发现,这个思路是有问题的,反例如下
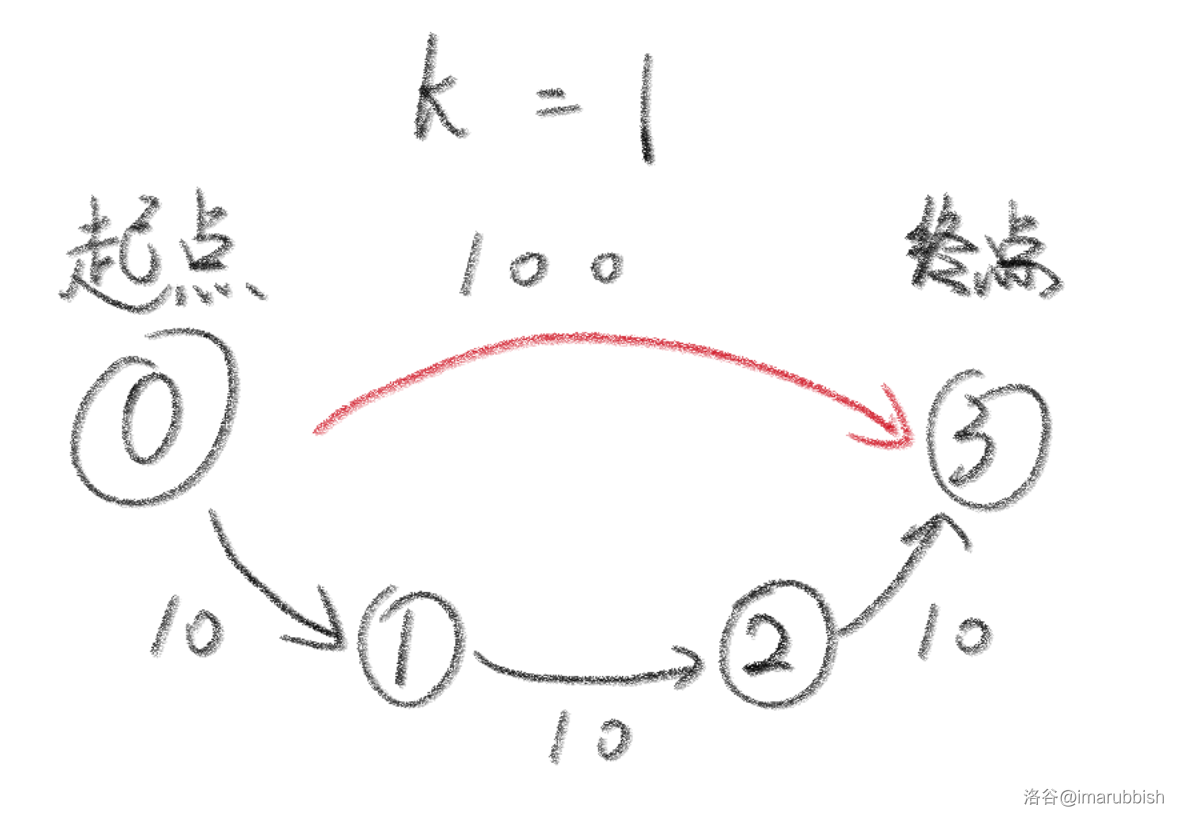
思路2:分层图
我们需要对原图进行一些改动,使其能够实现免费乘坐航班。其实很简单,每条航线添加一条费用为0的边即可。
但是,只有k次免费乘坐的机会,如何保证在求最短路的过程中免费乘坐航班的次数小于等于k呢?答案是建立一个分层的图。

将原图作为最上层,然后原封不动拷贝一份原图(编号+n)放在下面。对于原图中的每一条边都建立一条通往下一层的0费的边,以此作为免费乘坐航班的选项。这样一来,选择一次免费乘坐航班,就对应了在分层图中向下走一层。当然,终点由原图中的编号$t$变为了$t+kn$注意到数据范围$0 \le k \le 10$最多只需要10层即可。代码如下:
#include <bits/stdc++.h>
#define MAXN 100005
#define inf 0x3f3f3f3f
using namespace std;
int head[15 * MAXN], dist[15 * MAXN], cnt, n, m, k, s, t;
bool vis[15 * MAXN];
struct Edge
{
int to, next, dis;
}e[30 * MAXN];
struct node
{
int id, dis;
bool operator< (node const &a) const
{
return dis > a.dis;
}
};
void add_edge(int from, int to, int dis)
{
e[++cnt].to = to;
e[cnt].dis = dis;
e[cnt].next = head[from];
head[from] = cnt;
}
void Dijkstra(int start)
{
priority_queue<node> q;
q.push(node{start, 0});
for (int i = 0; i <= n + k * n; i++) dist[i] = inf;
dist[start] = 0;
while (!q.empty())
{
node x = q.top();
q.pop();
int now = x.id;
if (vis[now]) continue;
vis[now] = true;
for (int i = head[now]; i; i = e[i].next)
{
int y = e[i].to, d = e[i].dis;
if (dist[now] + d < dist[y])
{
dist[y] = dist[now] + d;
q.push(node{y, dist[y]});
}
}
}
}
int main()
{
int a,b,c;
cin >> n >> m >> k;
cin >> s >> t;
memset(head, 0, sizeof(head));
for (int i = 0; i < m; i++)
{
cin >> a >> b >> c;
add_edge(a, b, c);
add_edge(b, a, c);
for (int j = 1; j <= k; j++)
{
add_edge(a + j * n, b + j * n, c);
add_edge(b + j * n, a + j * n, c);
add_edge(a+(j-1)*n, b + j * n, 0);
add_edge(b+(j-1)*n, a + j * n, 0);
}
}
Dijkstra(s);
cout << dist[t + n * k];
}
这样看这个方法似乎已经完美了,可是提交之后发现有一个测试点过不了。提交记录
问题在于:最短路的算法可能在到达最下层之前(即用光免费乘坐次数之前)就已经到达终点,但是由于建图时的小缺陷导致到达$t+nk$反而要更多的花费。反例如下:
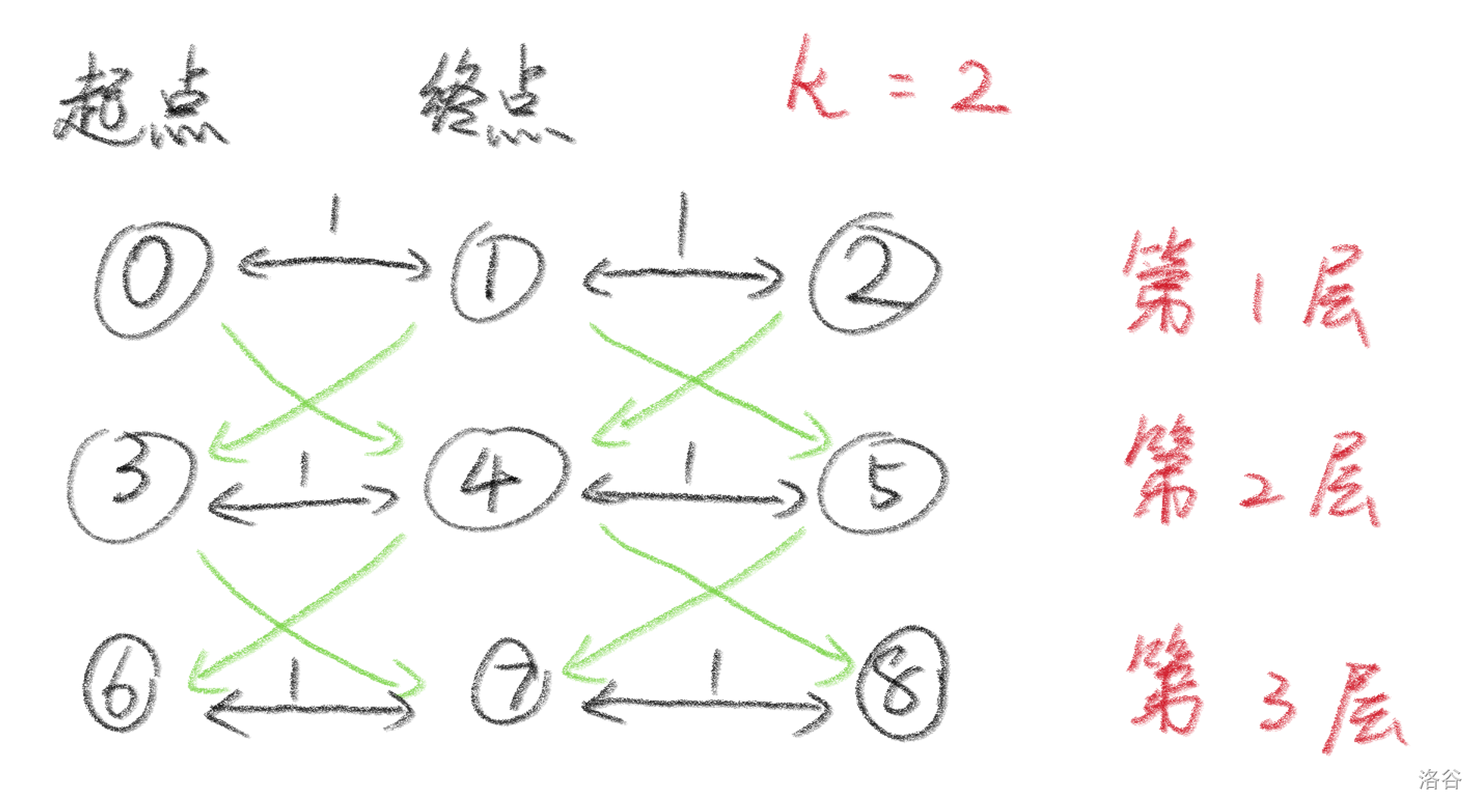
这个例子中,同样都是终点,到达7最少需要花费1,但是到达4只需要花费0。由此可见,若想要将$t+nk$作为终点,还需要把分层图中每一层的终点连起来。代码如下:
for (int i = 0; i < k; i++)
add_edge(t + i * n, t+(i+1)*n, 0);
最后附上AC提交记录: https://www.luogu.com.cn/record/146611433