极大似然译码实验报告

实验环境

编程语言：C++
依赖库：标准C++库
编译指令：std=c++17
编码：utf-8

实验内容

1. 群码的构造

1.1 设计思路

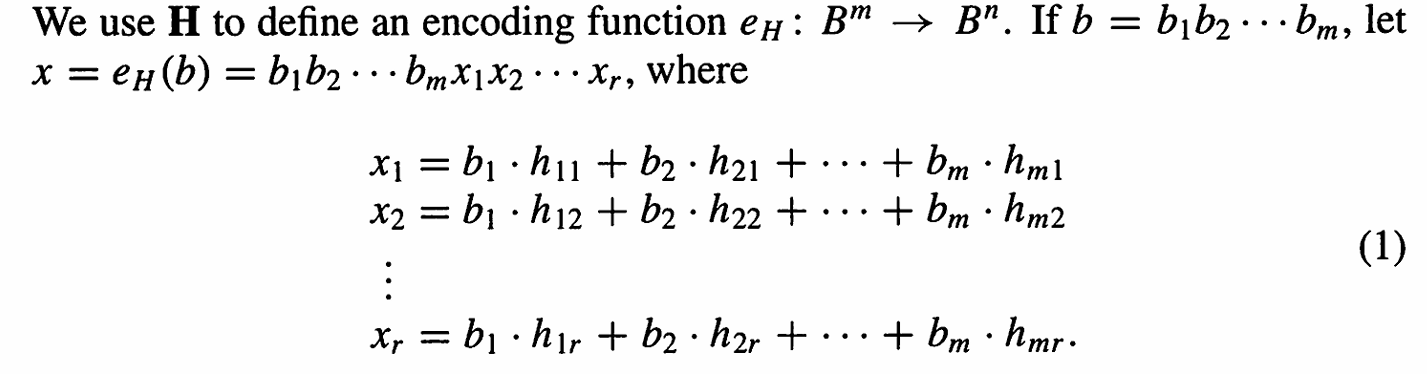
1.2 具体实现

// e和d分别为编码函数和译码函数，类型为map<int,int>
void Encoding::init(int m, int n, Matrix &H) {
    for (int b = 0; b < (1 << m); b++) {  // 遍历所有原码
        int eb = b;
        // 计算编码函数中x1, x2, ... , xr的值
        for (int j = 0; j < n - m; j++) {
            int x = 0;
            for (int i = 0; i < m; i++) {
                x ^= int(bool((1 << i) & b)) * H[m - i - 1][j];
            }
            eb = (eb << 1) + x; // 每趟循环将eb左移并将计算得到的x的值附在eb后面
        }
        e[b] = eb; // 存储编码函数
        d[eb] = b; // 顺便存储部分的译码函数
    }
}

初始化：
- m 和 n 分别表示原码和编码的长度。
- H 为奇偶校验矩阵。
遍历所有原码：
- for (int b = 0; b < (1 << m); b++) 遍历所有可能的 m 位二进制数 b。
计算编码值：
- int eb = b; 初始化编码值 eb 为 b。
- for (int j = 0; j < n - m; j++) 遍历 n - m 位，计算 eb 的每一位。
- for (int i = 0; i < m; i++) 遍历 m 位，计算 x 的值。
- eb = (eb << 1) + x; 更新 eb。
存储编码和解码结果：
- e[b] = eb; 将原码 b 和其对应的编码值 eb 存储在编码表 e 中。
- d[eb] = b; 将编码值 eb 和其对应的原码 b 存储在解码表 d 中。

2. 左陪集

2.1 设计思路

在群码中，$N = e_H(B)$ 是 $B^n$ 的正规子群。
寻找译码表中没出现过的元素 $x\in B^n$。
$xN$ 即为左陪集。
按照要求对译码表中的顺序进行整理。

2.2 具体实现

Matrix Encoding::getLeftCosetTable() {
    Matrix table(1 << (n - m), 0);
    vector<bool> vis(1 << n);              	// vis维护已经处理过的数
    // 遍历所有B^n中的数i；j为译码表的行号
    for (int i = 0, j = 0; i < (1 << n) && j < (1 << (n - m)); i++) {  
        if (!vis[i]) {                    	// 如果当前的数未被处理过
            for (auto [b, eb] : e) {       	// 遍历编码函数（译码表第一行）
                table[j].push_back(eb ^ i); // 存储左陪集
                vis[eb ^ i] = true;        	// 记录处理过的数
            }
            // 陪集头为左陪集中权值最小的那个数，使用lambda表达式得到
            int head=*min_element(table[j].begin(),table[j].end(),[](int a,int b)
            {
                return __builtin_popcount(a) < __builtin_popcount(b);
            });
            table[j][0] = head;  // 把陪集头放到第一列
            for (int k = 0; k < (1 << m); k++) {
                // 用陪集头和首行的异或值整理当前行
                table[j][k] = table[j][0] ^ table[0][k];  
                d[table[j][k]] = d[table[0][k]];          // 顺便处理译码函数
            }
            j++;  // 行号加1
        }
    }
    // 按照题目要求对译码表的行进行排序
    sort(table.a.begin(), table.a.end(), [](vector<int> &a, vector<int> &b) {
        if (__builtin_popcount(a[0]) == __builtin_popcount(b[0]))
            return a[0] < b[0];  // 若陪集头权值相同，按照大小排序
        else                     // 否则，按照权值排序
            return __builtin_popcount(a[0]) < __builtin_popcount(b[0]);
    });
    return table;
}

初始化：创建一个矩阵 table 和一个布尔向量 vis，用于记录已经处理过的数。
遍历所有可能的输入：遍历所有 B^n 中的数 i，并用 j 记录当前译码表的行号。
处理未处理过的数：如果当前数 i 未被处理过，则遍历编码函数 e，计算左陪集并记录。
确定陪集头：找到当前陪集中权值最小的数作为陪集头，并将其放在第一列。
整理当前行：根据陪集头和第一行的异或值整理当前行。
排序：按照陪集头的权值和大小对译码表的行进行排序。

3. 译码

3.1 设计思路

找到需要译码的 $x_t$ 所在列。
找到译码表中所在列的第一行元素 $e(b)$。
根据编码函数寻找 $e(b)$ 的原码 $b$。
$b$ 即为极大似然译码的结果。

3.2 具体实现

在前两个部分（1.2构造群码，2.2左陪集）中，已经顺便处理好了译码函数d，因此无需额外进行处理。

4. 校验子表

4.1 设计思路

利用函数$\mathrm{f_{H}:B^{n}\rightarrow B^{r},~f_{H}(x)=x^{*}H}$，得到每个陪集头的特征值。

4.2 具体实现

int Encoding::getSyndrome(int x) {
    int syn = 0; // 初始化特征值为0
    for (int j = 0; j < n - m; j++) { // 遍历奇偶校验矩阵每一列
        int y = 0;
        // 计算特征值的当前位y
        for (int i = 0; i < n; i++) {
            y ^= bool((1 << i) & x) & H[n - i - 1][j];
        }
        syn = (syn << 1) + y; // 更新特征值
    }
    return syn;
}

初始化：特征值 syn 初始化为 0。
遍历奇偶校验矩阵：外层循环遍历奇偶校验矩阵 H 的每一列。
计算当前位：内层循环计算特征值的当前位 y，通过按位与和异或操作实现。
更新特征值：将当前位 y 附在特征值syn的后面。
返回结果：返回最终计算得到的特征值 syn。

5. 特征值译码

5.1 设计思路

计算待编码的数 $x_t$ 的特征值。
查找与 $x_t$ 特征值相同的陪集头 $\epsilon$ 。
计算 $x_t \oplus \epsilon$ 得到 $e(b)$。
在编码函数中找到 $e(b)$ 的原码 $b$。
$b$ 即为极大似然译码的结果。

5.2 具体实现

for (int i = 0; i < (1 << (n - m)); i++) { 				// 遍历译码表的每一行
    int header = E.coset_table[i][0]; 					// 行首的元素为陪集头
    if (E.getSyndrome(header) == E.getSyndrome(x)) {	// 查找特征值相等的陪集头
        cout << " e=" << E.toBinary(header, n);
        eb = header ^ x; 								// 计算得到e(b)
        break;
    }
}
for (auto [b, _eb] : E.e) { 							// 遍历编码函数查找e(b)的原码b
    if (eb == _eb) {
        cout << " d(" << E.toBinary(x, n) << ")=" << E.toBinary(b, m) << endl;
        break;
    }
}

遍历译码表：
- 使用 for 循环遍历译码表的每一行。
- 每一行的行首元素 header 是陪集头。
- 检查 header 的特征值是否与输入 x 的特征值相等。
- 如果相等，输出 header 的二进制形式，并计算 e(b)。
查找原码：
- 遍历编码函数 E.e，查找与 e(b) 对应的原码 b。
- 如果找到匹配的 b，输出解码结果。

改进思路

在实验4和实验5中，代码的具体实现当中，校验子依靠陪集头得到，而陪集头通过译码表得到。也就是说，已经预先求出了译码表。通过特征值进行译码时，实际上并不需要整个译码表，可以在不求出译码表的情况下得到校验子表，节省程序运行所需的空间。

API文档

1. Matrix类

1.1 成员函数

Matrix()：默认创建函数，初始化为空矩阵。
Matrix(int n, int m)：带参数的构造函数，初始化矩阵大小。
void read(void)：从标准输入读取矩阵数据。
void print(void)：打印矩阵数据到标准输出。

1.2 特殊成员函数

vector<int> &operator[](int i) { return a[i]; }：重载operator[]，直接支持 matrix[i][j] 的形式访问矩阵元素。

2. Encoding类

2.1 成员函数

Encoding(int _m, int _n, Matrix &_H)：初始化$\rm Encoding$对象；计算编码函数 e，将输入的消息位映射为编码值；计算左陪集 coset_table；生成校验矩阵 H，对矩阵进行扩展形成标准校验矩阵，即：

\[Hinit=[P],P\in\{0,1\}_{m\times(n−m)}\] \[H=[P|I],P\in\{0,1\}_{m\times(n−m)},I\in\{0,1\}_{(n−m)\times(n−m)}\]

string toBinary(int num, int len)：使用按位与操作，将一个整数 num 转换为长度为 len 的二进制字符串。
map<int, int> getEncodingFunction：遍历所有可能的消息 b，利用校验矩阵 H 计算对应校验位。其中，校验位按行列乘法计算（逐位异或），结果附加到消息后形成编码值，即：

\[bP[i]=\oplus {b[j]\cdot P[j][i]},i=1,2,\ldots,n−m\] \[e=\{(b,e(b))∣b\in \{0,1\}_m\}\]

toDecimal(string num)：将二进制字符串转换为十进制数。
Matrix getLeftCosetTable()：计算左陪集表。维护一个用于标记是否在陪集中的向量，优先选择权值最小的未访问码字作为新陪集的头元素，即：

\[C(i)=\{e(b)\oplus i∣b\in Message Space\},i\in\{0,1,\ldots,2n−1\}\] \[Head(C(i))=argx\in C(i)\operatorname{min}Ham(x)\]

   对生成的陪集按照头元素的权值从小到大排序，如果权值相同，按照二进制大小排序（相当于按照题目要求的十进制大小排序）。

int getSyndrome(int x)：计算输入码字 x 的校验码，即对校验矩阵 H 与码字 x 的矩阵乘法结果（逐位异或），即： $Syn(x)=H\cdot x^Tmod2$

\[Syn(x)[i]=\oplus H[i][j]\cdot x[j],i=1,2,\ldots,n−m\]

此外，还有若干针对计算结果的输出函数。

3 主要函数

void test()：用户交互测试函数，用于获取输入和进行译码。我们将所有（共五个）题目的测试函数置于同一程序文件中。分别验证各个题目的代码时，将$\rm main()$函数中相应的测试函数注释或取消注释即可。

其中，void test1()到void test5()分别为构造、左陪集、译码、校验子表、特征值译码，与原题目顺序相同。

所有测试函数的输入、输出格式均与样例相符。

注意事项

代码中使用了C++17的一些特性，建议使用c++17及以上的版本进行编译。
代码中含有中文注释，建议使用$\rm utf-8$编码打开。
测试功能前，请确认是否取消了正确的测试函数的注释。

源码下载链接

上篇井字棋游戏

下篇跨年倒计时