Educational Round 166
D. Invertible Bracket Sequences
括号匹配题,除了用栈来考虑外,还有一个经典trick,可操作性更强。从左往右考虑,如果遇到左括号就+1,遇到右括号就-1,如果这个值在遍历整个串时一直大于等于0且在最后等于0就说明这个括号序列是合法的。如果画出一个图会更清晰,如下(抄自一篇洛谷题解):
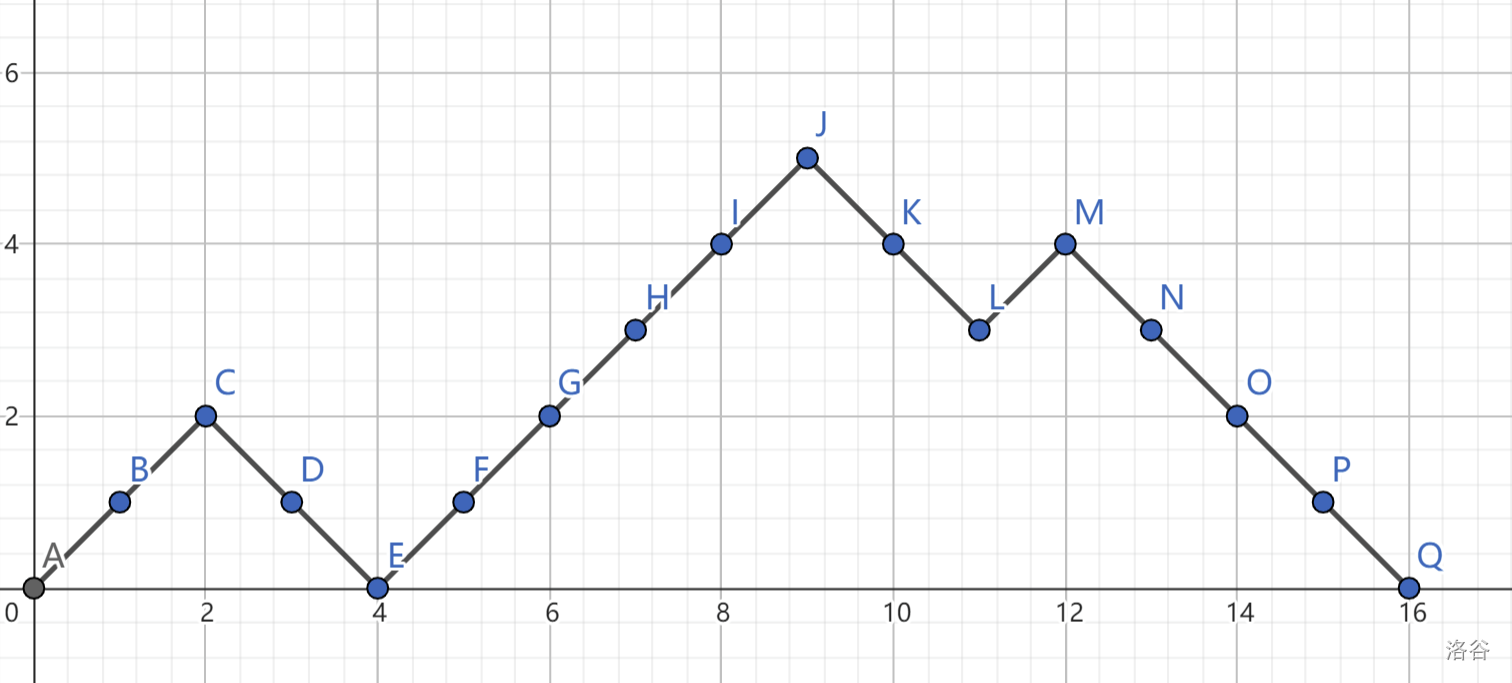
这张图对应的括号序列为:(())((((())())))
现在,我们反转某一区间的括号,相当于把这张图上的一段曲线向下翻折。我们要保证的是:
- 这段曲线在翻折后依旧是连续的
- 不能翻折到第四象限
第一点要求我们取两个 $y$ 坐标相同的地方进行翻折;第二点要求我们翻折的区间的最大值 $y_{max}$ 不能大于两倍的 $y$.
根据以上条件,我们现在考虑如何计数。
针对第一个条件,我们预先存储 $y$ 的值对应的下标即可。现在只需满足第二个条件。
我们枚举区间端点 $l$,考虑 $r$ 从 $l + 1$ 遍历到 $n$,这时区间 $[l, r]$ 的最大值具有单调性,我们可以对其进行二分,保证区间最大值如果往下翻不会翻到第四象限即可。如果我们可以在 $O(1)$ 求出区间最大值的话,总的复杂度将会是 $O(n \cdot log{n})$。这提示我们使用ST表进行维护。
总结一下,我们使用ST表维护区间最大值,预先处理好每个y值都有哪些下标,枚举区间左端点 $l$,二分找到使得 $[l,r]$ 区间最值不超过两倍 $y_l$ 的 $r_{max}$,然后统计 $y_l$ 所对应的在 $[l, r_{max}]$ 中的下标加入答案中。总的时间复杂度为 $O(n \cdot log{n})$。
Submission #300945572 - Codeforces
在洛谷的题解中,还有一个 $O(n)$ 的做法,是这样考虑的:
我们依旧从左向右遍历,并记录到目前位置为止 $y$ 的值为 $i$ 的下标出现了几次。记作a[i]。当y的值再次变成i的时候,我们此时还未更新 a[i],那么以当前下标作为右端点,就有 a[i] 个左端点可供选择。但是不要忘了需要保证最大值被翻下去时不能落到第四象限,这要求我们,当出现 $y$ 的值为 $2i+1$ 时,把 a[i] 清零。因为此时前面的所有 $y$ 值为 $i$ 的下标都不能再作为左端点了。也就是说,当前高度 $y$ 如果是奇数,我们需要把 a[y >> 1] 清零。这样就满足了上面说的两个条件,我们从左到右遍历一次统计答案即可。
Submission #300962768 - Codeforces(代码中y的值是用x表示的)
Luogu
P8663 倍数问题
我一开始想着排序,预处理之后枚举计数,感觉上可以,但是不太好写,细节比较多,而且写完只有50分。后来想着dp,从左向右考虑,dp[i][j] 表示由 i + 1 个数能组成的余数是 j 的最大值。然后考虑转移即可。
有一点需要注意,当我们考虑一个数 $a_i$ 时,要先统计答案,再转移 $dp_{1,j}$ 再转移 $dp_{0, j}$ ,否则会有重复使用 $a_i$ 的问题。
| [记录详情 - 洛谷 | 计算机科学教育新生态](https://www.luogu.com.cn/record/198250041) |