Educational Round 170
D. Attribute Checks
注意到m的值比较有限,只有5000,那么 $O(m^2)$ 是可以接受的。并且,从一个0到下一个0的过程中,能够通过的检查点是一个确定的值,如果我们知道此时的智力和力量值,并且预先对这些检查点做一些前缀和的预处理的话,可以在 $O(1)$ 时间内算出。那么我们只需枚举在每个0时的智力值然后进行状态转移即可。设 $dp_{i, j}$ 表示在第 $i$ 个0加点完成后拥有 $j$ 点智力,在到达第 $i + 1$ 个0之前能够通过的检查点的总数。然后考虑转移即可。受到空间限制,需要写int而不是long long,可以在原地处理前缀和来节省空间。
Luogu
P1641 生成字符串
这是一道和卡特兰数有关的问题。以我目前的知识来看,和卡特兰数相关的排列组合问题可以放在网格图上考虑。将卡特兰数定义为从 $(0,0)$ 到 $(n, n)$ 只能向右或向上走,且不能越过 $y=x$ 的路径数。如果不考虑 $y=x$ 的条件,那么总共有 $C_{2n}^n$ 种路径(考虑在 $2n$ 个向右指的首尾相接的向量中选择 $n$ 个向量把它变成向上指的向量)。一旦越过 $y=x$,则必然会到达 $y = x + 1$。我们将接触 $y = x + 1$ 之后的路径关于 $y = x + 1$ 做对称,那么终点就从 $(n, n)$ 变成了 $(n - 1, n + 1)$。也就是说,所有越过 $y = x$ 的路径数共有 $C_{2n}^{n+1}$ 个。所以卡特兰数 $H_n = C_{2n}^{n} - C_{2n}^{n + 1}$。
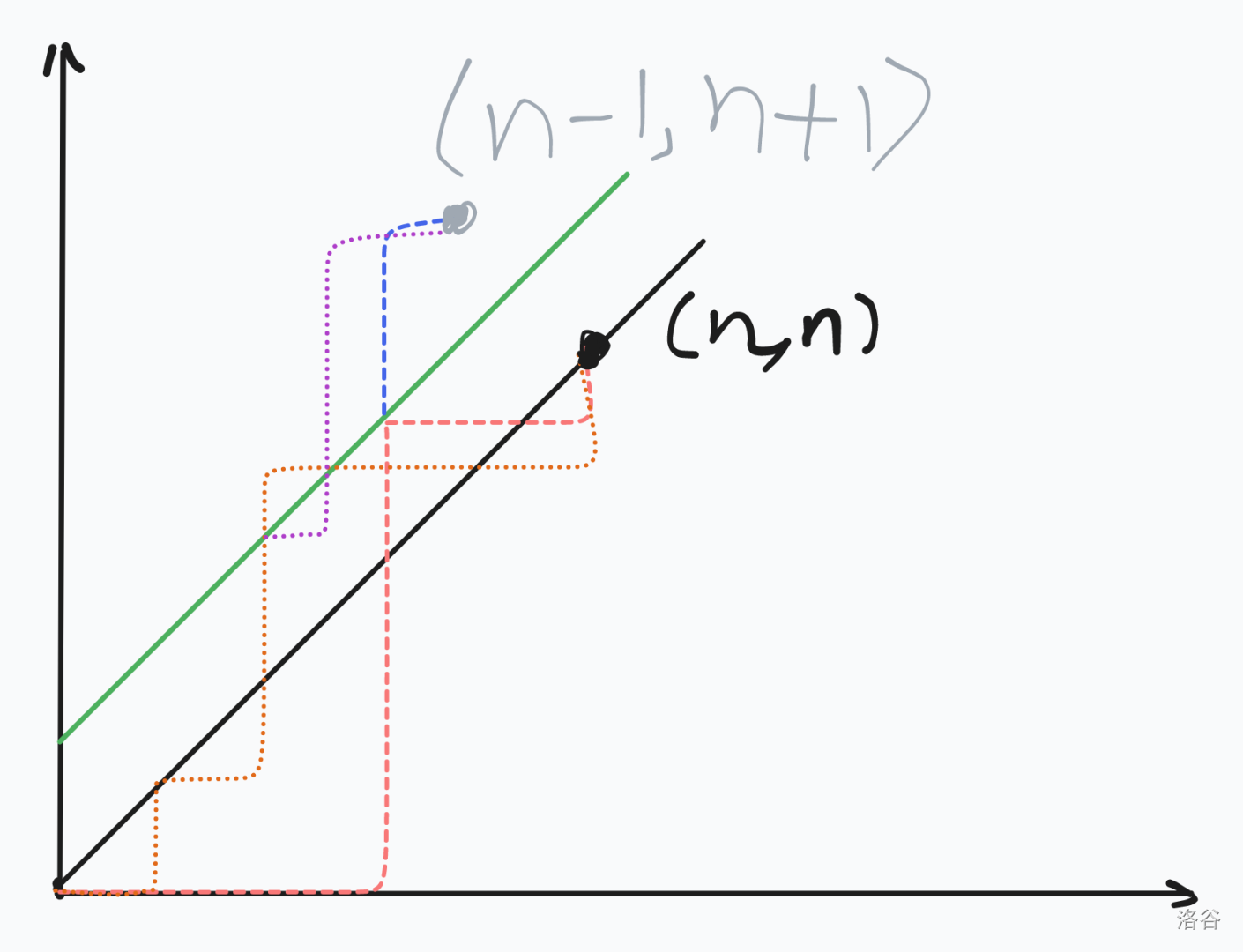
现在回到这道题。这道题可以等价于网格图上从 $(0,0)$ 走到 $(n, m)$ 且不越过 $y = x$ 的路径数,也就是 $C_{n+m}^{n}-C_{n+m}^{m+1}$。
值得一提的是,这道题我把n和m的顺序读反了,导致一直只有20分。这也是为什么1月15日的题解拖到1月16日才写的原因。
| [记录详情 - 洛谷 | 计算机科学教育新生态](https://www.luogu.com.cn/record/198479513) |
Educational Round 170
E. Card Game
这道题我首先想的是,如果只有一种花色,方案数有多少。其实这就是卡特兰数。我们这么想,总共有m种等级,并且m是偶数。那么不妨设 $m=2n$。而在卡特兰数对应的网格图上,向右的线段和向上的线段数量相等,如果我们把所有线段按照路径从 $(0,0)$ 到 $(n,n)$ 依次编号的话,可以保证向上的线段的编号总是能保证都大于向右的线段的编号,这也就和我们的出牌对应上了。也就是说这一方案数是 $H_{m/2}$。
现在我们考虑王牌花色1。设 $f_{i,j}$ 表示考虑到第 $i$ 种花色 使用了 $j$ 张花色1的方案数。那么有状态转移: \(f_{i,j}=\sum_{k\leq j}f_{i-1,j-k}\times T(k)\) 其中,$T_k$ 表示第 i 个花色的牌组种使用 $k$ 张花色 $1$ 的方案数,这个相当于网格图上先向右走 $k$ 步,也就是从 $(k,0)$ 到 $(\frac{m+k}{2},\frac{m+k}{2})$ 且不能越过 $y=x$ 的方案数,也就是 $T_k=C_{m}^{\frac{m+k}{2}} - C_{m}^{\frac{m+k}{2}+1}$。
现在,对于 $f_{n,k}$ 来说,我们还需要考虑从花色 $1$ 取出 $k$ 张牌的方案数。这和 $T_k$ 是相同的。
所以最终的答案为 \(\sum_{k \leq m}{f_{n,k}\cdot T_k}\)
Educational Round 121
C. Monsters And Spells
把每个monster看成以 $(k_i,0)$ 为直角顶点,$\geq h_i$ 为高的45°直角三角形。我们需要求的是这些直角三角形最小覆盖的离散面积。使用栈来维护三角形的直角边,每次入栈前把能出栈的都弹出栈,如果当前的这条直角边不够高,那就把它加高,然后把上一条弹出去。在处理时,一定要先出栈再来考虑入栈,并且用pii同时维护坐标和高度,这样比较好处理。